2020-CS310-January#

Your mark will be based on your best three answers All questions carry equal marks. 四选三

Part 1#

A compiler typically has two phases: front-end and back-end. Briefly discuss the functionality of each phase.

编译器概念

The analysis part (front end) breaks up the source program into pieces and imposes a grammatical structure on them. It uses this structure to create an intermediate representation of the source program. 分析部分(前端)将源程序分解成小块，并对其施加语法结构。它使用这个结构来创建源程序的中间表示。
The synthesis part (back end) constructs the desired target program from the intermediate representation and the information in the symbol table. 合成部分(后端)从中间表示和符号表中的信息构造所需的目标程序。

Why most of the lexical analyzers prefer using DFA rather than NFA.

DFA 的运行复杂度相比于 NFA 更加可控？

Outline the pseudo code for subset construction. Input: An NFA $N$. Output: A DFA $D$ accepting the same language.

Apply subset construction for the NFA (from Thompson’s construction) that accepts the following regular expression. Note that you need to clearly show $\epsilon$-closure computation for each step. $$ (0|1)*011 $$

NFA -> DFA

Part 2#

Use an algorithm to eliminate all left recursions in the following grammar. $$ S\rightarrow Aa|b\ A\rightarrow Ac|Sd|\epsilon\ $$

消除左递归

First, eliminate the left recursion of A->Sd->Aa,

Mathematica
"input the S to A"
A -> Ac|(Aa|b)d|ϵ
A -> Ac|Aab|bd|ϵ

A -> bdA'|A'
A'-> cA'|abA'|ϵ

Then we get a grammar like that,

Mathematica
S -> Aa|b
A -> bdA'|A'
A'-> cA'|abA'|ϵ

The production of A -> Ac contains a left recursion, split it as the following state,

Mathematica
A -> A'
A'-> cA'|ϵ

Construct an LL parsing table for the following grammar, $$ E\rightarrow E+T|T\ T\rightarrow T*F|F\ F\rightarrow (E)|id\ $$ You need to clearly show FIRST and FOLLOW sets for each non-terminal during the computation.

构造 LL 文法解析表

Eliminating the left recursion of above grammar, the new grammar is like that,

Mathematica
E -> TE'
E'-> +TE'|ϵ
T -> FT'
T'-> *FT'|ϵ
F -> (E)|id

Construct the FIRST set and FOLLOW set,

Mathematica
FIRST(E) = 
FIRST(E')= 
FIRST(T) = 
FIRST(T')= 
FIRST(F) = 

Split this grammar,

Mathematica
E -> E + T
E -> T
T -> T * F
T -> F
F -> (E)
F -> id

For the above grammar, the FIRST and FOLLOW set is as follows,

Mathematica
FIRST(E) = FIRST(T) = {(,id}
FIRST(T) = FITST(F) = {(,id}
FIRST(F) = {(,id}

Mathematica
FOLLOW(E) = {+,$} + {)} + FOLLOW(T)/{ϵ} 
      = {+,*,),$}
FOLLOW(T) = {*} + FOLLOW(E)/{ϵ} = {+,*,),$}
FOLLOW(F) = FOLLOW(T) = {+,*,),$}

Then we can construct the predictive parse table as follows,

	$+$	$*$	$($	$)$	$\$$
$E$
$T$
$F$

Part 3#

Using an example to illustrate the difference between a concrete syntax tree and an abstract syntax tree.

Answer

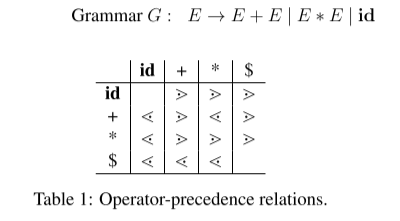
Table 1 shows the operator-precedence relations for grammar G. Show how to [6 marks] use these precedence relations to parse the input string: $id + id ∗ id$

Give the following type constructors array(S, T) and pointer(T),

array(S, T) : the type of an array with elements of type T and index set S. pointer(T) : the type “ pointer to an object of type T ”.

use them to design type checking rules for the following expressions. Note that each non-terminal E has an synthesised attribute type.

Give an algorithm (pseudo code) sequiv(s, t) that can be used for testing struc- [9 marks] tural equivalence of arrays, products, pointers and functions. Note that the algorithm should only use the following type constructors:

array(S, T) : product(T1, T2) : the type of an array with elements of type T and index set S. returns T1 × T2, if T1 and T2 are type expressions. function(D, R) : maps a domian type D to a range type R. pointer(T) : the type “ pointer to an object of type T ”.

Part 4#

Briefly outline the pseudo code of an algorithm that can solve register allocation [10 marks] (graph colouring) problem. Note that we define a graph as G = (V, E), where V is the set of vertices (available registers) and E is the set of edges.
Translate the following code into Java bytecode, using the notation generated [10 marks] by javap (Java bytecode instructions are provided in Table 2).

Java
public static int fun (int n) { 
    int s = 1; 
    for (int i=1;i<=n;i++) s = s*i;

 return s;
}

Illustrate the difference between a compiled language and an interpreted one. [5 marks] Is Python compiled or interpreted and why ?

最后更新: March 16, 2024
创建日期: March 16, 2024

	\(+\)	\(*\)	\((\)	\()\)	\(\$\)
\(E\)
\(T\)
\(F\)