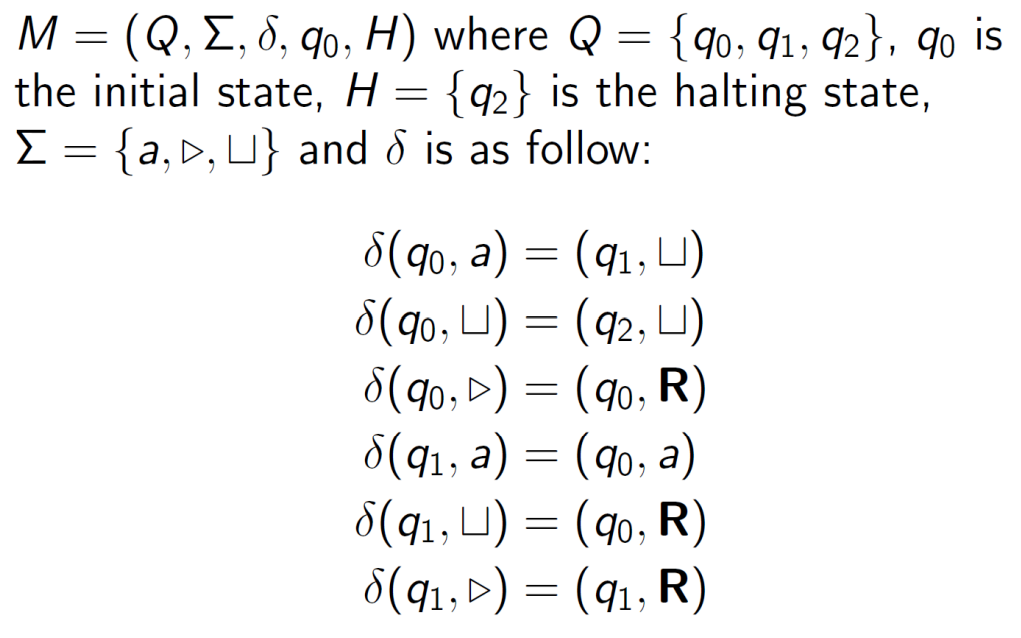跳转至

Overview#

  • Sets,Relations, and Languages (Mathematical basis)
  • Turing machines (Advanced computing machine model)
  • Undecidability
  • Computational Complexity
  • NP-completeness

Chapter 1 Sets, Relations, and Languages#

1.1 Set#

Summary

  • A set is a collection of objects
  • Set notation
  • Ideas to prove that sets are equal
  • On various operations and properties of sets • Power set
  • Partition

1.2 Relation And Function#

通过将二元关系作为一组有序对的概念，从集合 A 到集合 B 的函数是 A 和 B 上的二元关系 R，具有以下特殊性质：对于每个元素 a ∈ 𝐴 恰好有一个 R中的有序对与第一个组件a。

Example

Let C be the set of cities in the United States and let S be the set of states $$ R_1 = {} $$ A: Then R1 is a function, but R2 is not a function.

在这里我的个人理解是，R 这个描述 A 和 B 之前关系的

有三个主要的概念，设 A 和 B 是两个集合，\(f\) 是从 A 到 B 的函数。

  • one-to-one 一对一映射。如果 \(f\) 从不将两个不同元素映射到同一个对象，即只要 \(a\neq b\)，就有 \(f(a)\neq f(b)\)，则称 \(f\) 是一对一映射。
  • onto 满映射。如果 \(f\) 能击中 B 中的每个元素，即对 B 的每个元素 b，都存在 \(a\in A\)，使得 \(f(a)=b\)，则称 \(f\) 是满映射。
  • correspondence 对应。在对应中，A 的每个元素映射到 B 的唯一一个元素，且 B 的每个元素都有 A 的唯一一个元素映射到它，就是同时成立 one-to-one 和 onto 关系。

one-to-one = injective 单射

onto = surjective 满射

correspondence = bijective 双射

1.3 Special Types of Binary Relations#

Summary

  • directed graph
  • equivalence relation: reflexive, symmetric, and transitive
  • partial order: reflexive, antisymmetric , and transitive
  • path

1.4 Finite and Infinite Sets#

Summary

  • Equinumerous
  • Countable: finite set and countably infinite set
  • Uncountable: uncountably infinite set

1.5 Three Fundamental Proof Techniques#

The main purpose of this section is to introduce three fundamental proof techniques : mathematical induction 数学归纳, the pigeonhole principle 鸽巢原理, and diagonalization 对角线方法.

The Principle of Mathematical Induction: Let A be a set of natural numbers such that,

  1. \(0\in A\), and
  2. for each natural number n, if \(\{0,1,\dots,n\}\), then \(n+1\in A\)

Then \(A = N\).

Example

Let us show that for any \(n\geq 0, 1+2+\dots+n=\frac{n^2+n}{2}\).

image-20220901151436816

The Pigeonhole Principle

If A and B are finite sets and \(|A|>|B|\), then there is no one-to-one function from A to B. In other words. If we attempt to pair off the elements of A (the “pigeons”) with elements of B (the “pigeonholes”), sooner or later we will have to put more than one pigeon in a pigeonhole.

鸽巢理论的意思就是，如果两个有限集合 A 和 B 之中，size(A) > size(B)，那么就不存在 A 对 B 的单映射，因为一定会有多出来的鸽子。

鸽巢理论一般使用反证法，在某一个假设的前提下，如果证明不了 A 和 B 之间的 one-to-one function，那么这个假设就被证伪。

Theorem 1.5.1: Let R be a binary relation on a finite set A , and let \(a, b\in A\). If there is a path from a to b in R , then there is a path of length at most \(|A|\). 设 R 为有限集 A 上的二元关系，设 \(a, b\in A\)。 如果在 R 中存在从 a 到 b 的路径，则存在长度最多为 \(|A|\) 的路径。

Proof:

Suppose that \((a_1,a_2,…,a_n)\) is the shortest path from \(a_1=a\) to \(a_n=b\), that is, the path with the smallest length, and suppose that \(n > |A|\) . By the pigeonhole principle, there is an element of A that repeats on the path, say \(a_i=a_j\), \(0<i<j<n+1\). But then \((a_1,a_2,…,a_i,a_{j+1},…a_n)\) is a shorter path from a to b, contradicting our assumption that \((a_1,a_2,…,a_n)\) is the shortest path from a to b.

在这边卡了好久，我大概理解为在证明中，我们一开始设了一个前提，为 \(|A|\) 个鸽巢中增加一个鸽子，这个鸽子就是 \(a_j\) ，它是一个重复的鸽子，这时总共的鸽子变成了 \(|A+1|\) 个，但是实际上最长的路径长度还是 \(|A|\)，因为 \(a_i = a_j\)，走其中一个是一样的，但没法同时走 \(a_i\) 和 \(a_j\)。

The Diagonalization Principle

Let \(R\) be a binary relation on a set \(A\), let \(D\), the diagonal set for \(R\), be \(D = \{a:a\in A\ and\ (a, a) \notin R\}\) For each \(a \in A\), let \(R_a = \{b:b\in A\ and\ (a, b) \in R\}\)

Then \(D\) is distinct for each \(R_a\).

对角论证法 - 维基百科，自由的百科全书 (wikipedia.org)

Lecture 2 Turing Machine#

2.1 Definition#

The basic idea of the Turing machine is a machine to compute a function \(f:A\rightarrow B\) voer an infinite tape.

  • The number of steps are finite
  • The number of symboles which it reads and write on the tape are also finite.

image-20220926225648008

Working Process

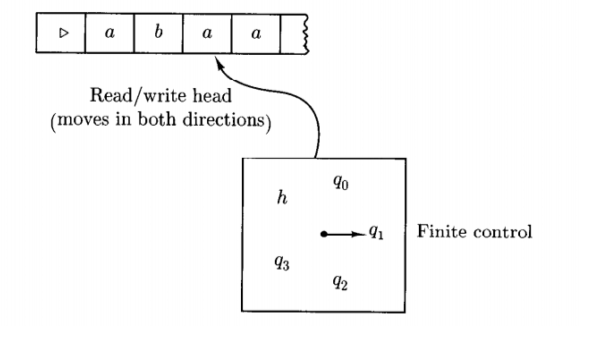
  • Each step of the computation depends on its current state and the tape symbol currently scanned by the read /write head 计算的每一步取决于其当前状态和读/写磁头当前扫描的磁带符号
  • By putting the control unit in a new state two senario will happens:
  • Either Write a symbol in the tape squre currently scanned, replacing the one already there 写入
  • Or Move the read/write head one tape square to the left or right. 或移动

Notation

Tape

The tape has a left end, but it extends indefinitely to the right. 左端有尽头，右端无限延伸。

To prevent the machine from moving its head off the left end of the tape, we assume that the leftmost end of the tape is always marked by a special symbol denoted by \(\rhd\). 定义最左端标记符

We assume further that all of our Turing machines are so designed that, whenever the head read a \(\rhd\), it immediately moves to the right. 只要头读到 \(\rhd\) 则向右移动。

We use the distinct symbols \(L\) and \(R\) to denote movement of the head to the left or right. 移动方向表示符的定义

The rest of the tape initially contains blank symbols, denoted \(\sqcup\). 定义空白符号，tape 上最初全是空白符

Turing Machine

A TM (Turing Machine), is a 5-tuple \((Q,\varSigma,\delta,s,H)\).

  • \(Q\) is the finite set of states; 有限状态集

  • \(\varSigma\) is an alphabet that contains \(\sqcup\) and \(\rhd\) but not containing the symbols \(L\) and \(R\); 字母表，包含空白符起始符，但是不包含移动符

  • \(s \in Q\) is the initial state; \(s\) 是初始状态

  • \(H\) is the set of halting states; \(H\) 是终止状态集

  • \(\delta\) is the transition function $$ \delta:(Q\textbackslash H)\times\varSigma\rightarrow Q\times(\varSigma \cup{L,R}) $$

  • if \(\delta(q,\rhd)=(p,b)\) then \(b=R\),

  • if \(a\in\varSigma\) and \(\delta(q,a)=(p,b)\) then \(b\neq\rhd\).

Another form,

image-20220927010809289

Example

image-20220927090152434

如以上例子中 \(\delta(q_0, a) = (q_1, \sqcup)\) 中，\(q_0,q_1\) 是当前状态与下一状态，\(a, \sqcup\) 是属于字符表 \(\varSigma\) 的字符，前一个为读到的字符，后一个为写入的字符。当然因为操作不只有写入操作，也包括移动操作，所以第二位也可能是 \(L\) 或 \(R\) 这两个位移符。

Configuration 格局#

We break the string on tape at each state into two pices.

The part to the left of the scanned square, including the single symbol in the scanned square;

And the part, possibly empty, to the right of the right of the scanned square.

Notation

Configuration of TM

A configuration of a Turing Machine \(M=(Q,\varSigma,\delta,s,H)\) is a member of \(Q\times\rhd\varSigma^*\times(\varSigma^*(\varSigma\textbackslash\{\sqcup\}\cup\{\varepsilon\}))\)

这样的记法有几个特征，可以先看看几个例子，

  • \((q,\rhd a, aabbb)\)
  • \((q,\rhd\sqcup\sqcup b, \varepsilon)\)
  • \((q, abb, ab)\)
  • \((q, \rhd abb,\sqcup bb\sqcup)\)

以上的例子中，前两个是正确的格局，后两个不是。这样的格局表示法第一个参数表示的是图灵机当前所处的状态；第二个参数是 tape 从最左的起始符开始的所有字符，但省略右端未使用的空白字符，所以这个参数一定是以 \(\rhd\) 开头的；第三个参数是表示输入字符，可以是除空白字符 \(\sqcup\) 以外的字符表内的所有字符以及表示任意输入的 \(\varepsilon\)。

另外还有一种简略写法，将 \((q, wa, v)\) simplify to \((q, w\underline{a}v)\)。Where underlined position indicates the head position. 下划线位置表示头部位置

Notation

Configuration of TM

For a Turing machine \(M = (Q, \varSigma, \delta, s, H)\) we say configuration \((q_1, w_1\underline{a_1}v_1)\) yield in one step configuration \((q_2, w_2\underline{a_2}v_2)\) and write \((q_1, w_1\underline{a_1}v_1)\)

Lecture 3 Undecidability#

3.1 The Church-Turing Thesis#

略

3.2 Universal Turing Machines#

略

3.3 The Halting Problem#

最后更新: March 16, 2024
创建日期: March 16, 2024