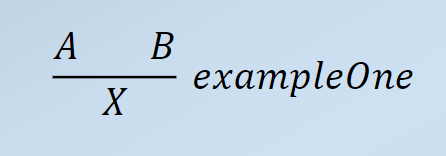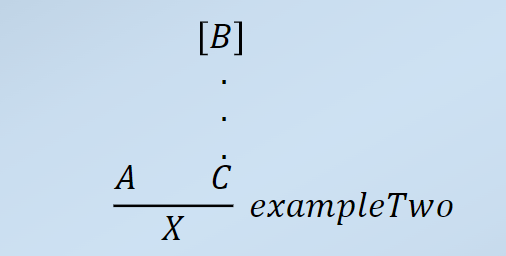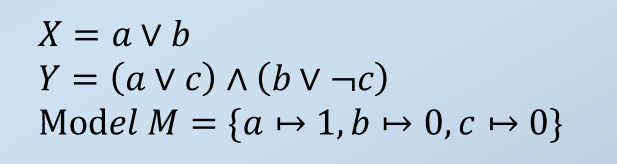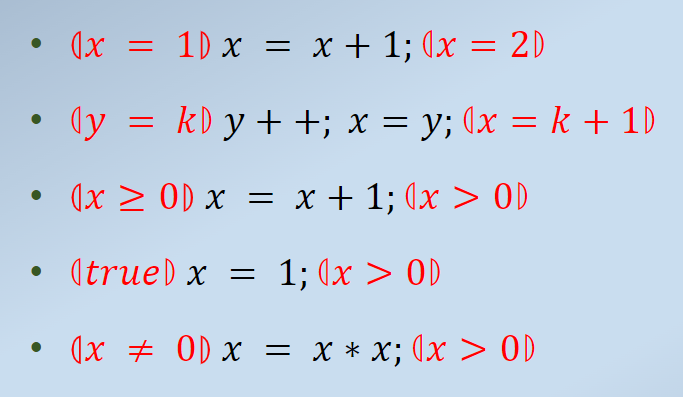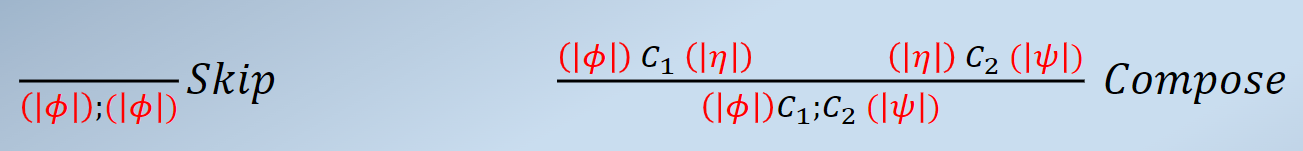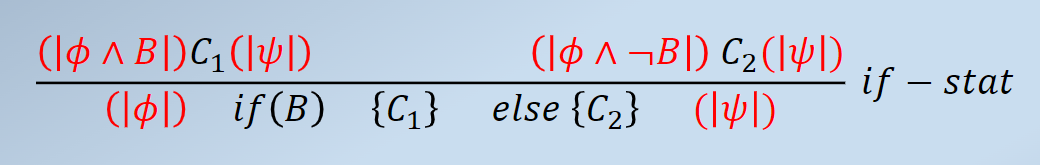Topic to be covered#
- Design by Contract
- Prop/FOL Proofs with Coq
- SAT/SMT Solvers
- Hoare Logic
- Prove your programs with Dafny
- Model Checking
Lecture 01 Introduction#
Motivations for software verification#
When you might want to verify your code:
- Safety-critical software like airplanes, nuclear power plants
- Programs with expensive failure consequences: e.g. space missions, stock exchange, ...
- Legal obligations
Verification compare to Testing: test can show the presence of bugs, but can't show absence.
Lecture 02 Design by Contract#
Design by Contract 契约式设计#
Design by Contract,中文译名 契约式设计,缩写为 DbC,通用名称是 Programming by Contract (因为 Design by Contract 是一个注册商标),也可以称为 Contract Programming,Contract-First development,Code Contract 代码合约。
DbC的核心思想是对软件系统中的元素之间相互合作以及“责任”与“权利”的比喻。这种比喻从商业活动中“客户”与“供应商”达成“契约”而得来。例如:
- 供应商必须提供某种产品(责任),并且他有权期望客户已经付款(权利)。
- 客户必须付款(责任),并且有权得到产品(权利)。
- 契约双方必须履行那些对所有契约都有效的责任,如法律和规定等。1
There are some possible pitfalls with the "conventional" approach, If without DbC:
- The client may not understand in what situations a method can be used 客户可能无法理解在什么情况下可以使用方法
- The client may not understand fully the consequences of running a method 客户可能无法完全理解运行方法的后果
- When the supplier changes the implementation, how do they ensure the interface is preserved? 当供应商更改实施时,他们如何确保保留接口 (在不破坏旧代码的前提下)
- If the interface does change, how does the supplier ensure some consistency? 如果接口发生变化,供应商如何确保某种一致性
Key Concept#
Every class has two "roles" associate with it:
- Supplier 供应商
Wrote the class code; documents it, maintains it; knows about the class implementation; publishes the class interface 编写类代码; 记录它,维护它; 了解类的实现; 发布类接口
- Client 客户端
Uses the class in their own code; reads the documentation (presumably); knows about the class interface; knows nothing about the implementation 在自己的代码中使用该类; 阅读文档(大概); 了解类接口; 对实现一无所知
Main Principle#
Main principles of DbC:
-
Every public method has a precondition and a postcondition 每个公共方法都有一个前置条件和一个后置条件
-
The precondition expresses the constraints under which the method will function properly 前提条件表示方法将正常运行的约束条件
-
The postcondition expresses what will happen when a method executes properly 后置条件表示当方法正确执行时会发生什么
Preconditions and postconditions are boolean-valued expressions i.e. they evaluate to true / false
Precondition 先决条件 前提 前置条件 相当于正确输入 Postcondition 后置条件 相当于正确输出
The Contract 合约#
定义前置条件和后置条件建立了从供应商到客户端的合约:
- 如果客户端在满足前提条件的情况下运行该方法
- 然后供应商将确保方法执行将始终提供满足后置条件的状态
Obligations and Benefits 义务和利益#
| Precondition 先决条件 | Postcondition 后置条件 | |
|---|---|---|
| Client | obligation: I must ensure the precondition is true before calling the method 义务:在调用方法之前,我必须确保前提条件为真 |
benefit: I'm guaranteed the postcondition will be established by the method 利益:我保证后置条件将由该方法建立 |
| Supplier | benefit: I can assume the precondition is true when writing the method 利益:我可以在编写方法时假设前提条件为真 |
obligation: I must ensure when I write the method that the postcondition is satisfied 义务:我必须确保在编写方法时满足后置条件 |
这个表格看着有点难懂,我的理解是,
- 客户端保证正确输入,但是默认正确输出
- 供应商默认正确输入,但是需要确保正确输出
Non-redundancy principle 非冗余原则#
The body of a method shall not check to see if the precondition is true 方法体不应检查前提条件是否为真
- This DBC principle is the opposite of defensive programming 此 DBC 原则与防御性编程相反
- DBC reduces overhead and complexity of those extra checks DBC 减少了这些额外检查的开销和复杂性
- Also: maybe the client has already checked the precondition (for some other purpose) - how many times do we have to check it? 另外:可能客户端已经检查了前提条件(出于其他目的) - 我们需要检查多少次?
Precondition Availability Rule 前提条件可用性规则#
Every feature appearing in the precondition of a routine must be available to every client to which the routine is available 出现在例程的前提条件中的每个功能都必须对每个可以使用该例程的客户端都可用
- This is a reasonable demand, since the client must establish the precondition before calling a method. 这是一个合理的要求,因为客户端必须在调用方法之前建立先决条件。
- So, for example, a method precondition should not refer to the private attributes of the class. 因此,例如,方法前置条件不应引用类的私有属性。
- Checking that this rule holds can be done by the compiler. 编译器可以检查该规则是否成立。
-
The same is not true for the postcondition - it may refer to private attributes (Why?) 后置条件并非如此——它可能指的是私有属性
-
这个看不懂,准备问人
Assertion 断言#
Assertions are not an input checking mechanism 断言不是输入检查机制
- Assertions are software-to-software contracts. 断言是软件到软件的合约
- They are not software-to-user checks, or software-to-device checks. 它们不是软件到用户的检查,也不是软件到设备的检查
- Erroneous input from devices/users should be dealt with by writing the appropriate code. 来自设备/用户的错误输入应该通过编写适当的代码来处理。
Assertions are not control structures 断言不是控制结构
- A properly-working, bug-free, piece of software should not throw assertions. 一个正常工作、没有错误的软件不应该抛出断言。
-
Your code not try to catch an assertion-exception and fix things. 您的代码不要试图捕捉断言异常并修复问题。
-
(compare: exceptions are not a control structure) 比较:异常不是控制结构
我接触到断言这一机制是在 Golang 中。在 Go 语言中,接口是非申明式的,如果某一个结构体实现了某一个接口约定的所有方法,则该结构体便是实现了该接口。同时,Go 语言的接口可以作为参数类型传入函数中,所有实现了该接口的结构体都可以作为这个参数的输入。但是如果想从接口中解析出指定的结构体该如何呢?这时候就是使用断言机制的时候。一个类型断言检查它操作对象的动态类型是否和断言的类型匹配。2
所以断言机制是对类型进行检查,这个机制不应该关心具体数值,而是判断在逻辑层面的错误。 主要也是现在很多语言都有动态类型,断言就是针对动态类型这样不确定的类型的操作?
Violating an Assertion#
What happens if an assertion (pre- or post-condition) is not satisfied? 如果断言 (前置条件或后置条件) 不满足会发生什么?
- Then when the code is run, an assertion is violated. This means there is a bug in the code. 然后当代码运行时,断言被违反。 这意味着代码中存在错误。
- An exception should be thrown, telling the user what assertion has been violated (i.e. where it is), and how it has been violated. 应该抛出一个异常,告诉用户什么断言被违反(即它在哪里),以及它是如何被违反的。
- If a precondition is violated, then the bug is in the client’s code 如果违反先决条件,则错误在客户端代码中
- If a postcondition is violated, then the bug is in the supplier’s code 如果违反了后置条件,则错误在供应商的代码中
这个就是通过断言机制来判断程序异常并进行排错的过程。
Class Invariants 类不变量#
A class invariant is just an assertion involving the (class and) instance variables 类不变量只是涉及 类和实例变量 的断言 (没懂)
- All objects of the class must satisfy the invariant at all stable times, i.e.:
- After the execution of any of the constructors 在执行任何构造函数之后
- Before and after the execution of every public method 在每个公共方法执行之前和之后
- Corollary (1): Private methods can violate the invariant 私有方法可能违反不变量
- Corollary (2): It is the class supplier’s job to make sure the constructors and public methods maintain the invariant 确保构造函数和公共方法保持不变是类提供者的工作
Consequences of the class invariant#
-
If you don’t define a constructor, then the default constructor (or the class initialization code) must establish the invariant 如果不定义构造函数,则默认构造函数(或类初始化代码)必须建立不变量
-
The class invariant is effectively and-ed with both the precondition and the postcondition of each public method. 类不变量与每个公共方法的前置条件和后置条件都有效地与。
- Consequences for the supplier when writing a public method 供应商编写一个公共方法的后果
- Benefit: can assume that the invariant holds at the start of the method 可以假设不变量在方法开始时成立
- Obligation: must ensure that the invariant holds at the end of the method 必须确保不变量在方法结束时成立
DbC and Inheritance 继承#
Inheritance 继承机制#
略
Example: What kind of precondition and postcondition should the deliver method in a subclass of Courier have?
Method Preconditions and Postconditions with Inheritance#
Preconditions When A is a superclass of B... 当A是B的超类
- Remember: the client must satisfy the precondition 客户端必须满足前提条件
- ... but the client doesn’t know the run-time type of the object 但客户端不知道对象的运行时类型
- ... so the client only knows about the preconditions of A-methods 所以客户端只知道 A 方法的先决条件
- Therefore: Preconditions of methods in B cannot demand more than preconditions of methods in A. (They may demand less) B中方法的前提条件不能比A中方法的前提条件要求更多。
In logic terms, an A-method’s precondition must imply the precondition of any overridden version of that method in B 在逻辑术语中,A 方法的前提条件必须暗示 B 中该方法的任何覆写版本的前提条件
Postconditions When A is a superclass of B...
- The supplier must ensure that every method establishes its postcondition 供应商必须确保每种方法都建立其后置条件
- Thus, every B-method that overrides an A method must (at least) establish the A-method’s postcondition 因此,覆盖 A 方法的每个 B 方法都必须(至少)建立 A 方法的后置条件
- It may establish more than this (e.g. properties relating to new variables in the class) 它可能会建立更多(例如与类中的新变量相关的属性)
In logic terms, a B-method’s postcondition must imply the postcondition of any overridden version of that method in A 用逻辑术语来说,B 方法的后置条件必须隐含任何 A 中该方法的覆写版本
Inheritance and class invariant 继承与类不变量#
Example,
| Java | |
|---|---|
If A is a superclass of B:
- B inherits all the (non-private) class invariants from A. B 从 A 继承所有(非私有)类不变量
- B may add a few of its own, either on: B 可能会添加一些自己的
- the inherited variables, 继承的变量
- or on new variables introduced by B 或 B 引入的新变量
In logic terms, B’s class invariants must imply A’s class invariants. 从逻辑上讲,B 的类不变量必须隐含 A 的类不变量。
Summary: DBC and Inheritance#
In summary, if A is a superclass of B, then you’re writing B, you can:
- strengthen the class invariant 加强类不变量
- weaken the precondition of overridden methods 削弱覆盖方法的前提条件
- strengthen the postcondition of overridden methods 加强覆盖方法的后置条件
But not the opposite!!!
Lecture 03 Example of DbC#
Lecture 04 Logic for Program Specification#
Outline#
- Introduction and History of Logic
- Propositional Logic
- Natural Deduction Rules
- Introduction to Coq Proof Assistant
Intro & History of Logic#
Logic is the study of systems which are governed by a set of precise and well-defined rules.
Logic, on the other hand, describes things by stating their properties. It also provides rules for working out new facts about things, given some starting information.
Propositional Logic#
Consider these two arguments,
- If the train arrives late and there are no taxis at the station, then John is late for his meeting. John is not late for his meeting. The train did arrive late. Therefore, there were taxis at the station.
- If it is raining and Jane dose not have her umbrella with her, then she will get wet. Jane is not wet. Therefore, Jane has her umbrella with her.
Both of these translate into the same argument,
| P | the train arrives late | it is raining |
| Q | there are taxis at the station | Jane has her umbrella with her |
| R | John is late for his meeting | Jane is wet |
Then the arguments become: $$ (P and \sim Q) \rightarrow R\ \sim R\ P\ =======\ Q $$
Proof: Notation and Terminology#
- Notation
- In math: \(H_1, H_2, \dots ,H_n \vdash G\)
- In Coq: \(H_1 \rightarrow H_2 \rightarrow \dots \rightarrow H_n \rightarrow G\)
- Meaning: Whenever all of \(H_1, H_2, \dots, H_n\) are true then so is G
- Each \(H_i\) is called a hypothesis (or a premise) 假设
- \(G\) is called the goal (or the conclusion) 目标
- Transitivity of implication 蕴涵传递性
Natural Deduction Rules#
"Natural Deduction" works on the structure of the predicates involved in a proof. 自然演绎作用于证明中涉及的谓词的结构。
-
You work step-by-step to manipulate the structure of the hypotheses and the goal so that they eventually match each other.
-
We have an introduction and elimination rules for each of the connectives and quantifiers
- We use elimination rules to break up the hypothesis.
- We use introduction rules to form the goal
Format of the Proof Rules#
If we write,
then we mean that:
- If we have already shown that A and B are true
- then this rule, called example One, allows us to deduce that X is true.
If we write something of the form:
then we mean that:
- If we have already shown that A is true, and if we have shown that when we assume B then C is also true
- then this rule, called example Two, allows us to deduce that X is true.
Here, B is a local or temporary assumption and it is discharged when we apply the rule. B在此处为一个假设,假设 B 成立,则 C 成立,则 A 与 C 皆为真,通过 example Two 这个规则可以得到 X。则该 Notation 表示为,当 B 成立时,X 成立。
Assumptions in natural deduction#
One of the most important facets of proof construction is keeping track of assumptions. 证明构造最重要的方面之一是跟踪假设。
我们在证明期间的某些阶段做出假设以处理某些情况 - 假设帮助我们模块化证明。
所有假设都应在证明结束时解除。
因为只有一些规则允许你解除假设,所以你应该只在决定使用这些规则之一之后才引入假设。
Intro to Coq Proof Assistant#
开始证明之前,通常需要声明一些命题变量,语法如下:
| Bash | |
|---|---|
然后你可以这样开始证明:
| Bash | |
|---|---|
在 Coq 显示 "Proof completed" 之后,可以输入以下语句来保存证明:
| Bash | |
|---|---|
Proof tactics in Coq#
There are two main tactics for dealing with implication in Coq:
- Introduction: The tactic intro takes a goal of the form \(P \rightarrow Q\) and makes P a hypothesis, and makes Q the new goal. The tactic intros will perform a series of intro commands.
- Elimination: If you have some hypothesis H of the form \(P \rightarrow Q\) then the tactic apply H implements implies-elimination, transforming a goal Q into the goal P.
Lecture 11 Intro to Automated Reasoning#
Outline#
Understand SAT/SMT solver
- Foundation
- Logic
- Satisfiability & Validity
- Normal Forms
- SAT Solver
- DPLL
- Examples
Logic#
- Logic is an effective way of reasoning. 逻辑是一种有效的推理方式。
- Formal logic: precise, syntactic well-formed expressions and correct deductions. 形式逻辑:精确、语法结构良好的表达和正确的演绎。
- It is possible to compute consequences at the symbolic level. 可以在符号级别计算后果。
-
Computers can be used to automate such symbolic computations. 计算机可用于自动化此类符号计算。
-
Logic studies the relationship between language, meaning, and proof method. 逻辑研究语言、意义和证明方法之间的关系。
- A logic consists of a language in which sentences are expressed. 逻辑由表达句子的语言组成。
- A semantic that distinguishes the valid sentences from the refutable ones. 区分有效句子和可反驳句子的语义。
- A proof system for constructing arguments justifying valid sentences. 用于构建论证有效句子的证明系统。
- Examples: propositional logic, first-order logic, higher-order logic etc. 示例:命题逻辑、一阶逻辑、高阶逻辑等。
LOGICAL LANGUAGE#
A logical language consists of symbols whose interpretations are fixed. 逻辑语言由解释固定的符号组成。 These symbols are combined together to form well-formed formulas. 这些符号组合在一起形成格式良好的公式。
Syntax of propositional Logic 命题逻辑语法
- Symbols
- Constants: \(TRUE, FALSE\)
- Variables: \(P, Q, R, \dots\)
- Connectives: \(\land, \lor, \neg , \rightarrow\)
- Sentences / Formulas
- Constructed from simple sentences
- Using connective to connect each sentence.
Syntax of First-order Logic 一阶逻辑语法
- Symbols
- Constants: \(TRUE, FALSE, ALICE, BOB\)
- Variables: \(x, y, z, \dots\)
- Predicates:
IsLeft(), IsRight()- Functions:
sqrt(int), sizeof(t), >- Connectives: \(\land, \lor, \neg, \rightarrow, \Leftrightarrow\)
- Quantifier: \(\forall, \exist\)
- Atomic Sentence
- Constructed from predicates or terms.
- Term is constructed from function or constant or variable.
sqrt(sqrt(x)) > sizeof(y)).
SATISFIABILITY & VALIDITY#
Describe the one term, theory
A theory \(T\) consists of a set of formulas (well-formed) \(F=\{F_1,F_2,\dots,F_n\}\). Each line in the truth table is an interpretation.
- If there exists one interpretation from the truth table that can satisfy \(\{F_1,F_2,\dots,F_n\}\), this interpretation is a model \(M\) satisfies \(T\).
- If there interpretation from the truth table that satisfy \(\{F_1,F_2,\dots,F_n\}\), we say \(T\) is valid.
- If all interpretations from the truth table that cannot satisfy \(\{F_1,F_2,\dots,F_n\}\), \(T\) is unsatisfiable.
- A propositional formula is valid iff its negation is unsatisfiable.
Example
\(a\vee b\rightarrow b\) satisfiable
a b \(a\vee b\) \(a\vee b\rightarrow b\) T T T T T F T F F T T T F F F T
我简单理解成这样
- 真值表的每一行都是一个 Interpretation。
- \(a\vee b\) 和 \(a\vee b\rightarrow b\) 是分别的两个 theory。
- a 和 b 的每一组输入组合都是一个 model。
- 关于 satisfiable unsatisfiable valid
- 当真值表结果部分为真,则该 theory 是 satisfiable。
- 当真值表结果全为真,则该 theory 是 valid。
- 若 formula 为 valid,则这个 formula 的反为 unsatisfiable。
- 当真值表结果全为假,则该 theory 是 unsatisfiable。
Equisatisfiable#
Given two formulas 𝑋 and 𝑌, we say they are equisatisfiable if and only if 𝑋 is satisfiable if and only if 𝑌 is.
Example
对于同一个 \(M\),formula \(X\) and formula \(Y\) are same result 1, they are satisfiable for model \(M\). Therefore, X and Y equisatisfiable.
But, they are not equivalent.
Equisatisfiability is weaker than equivalence.
Normal Forms#
A formula where negation is applied only to propositional atoms is said to be in Negation Normal Form (NNF). 否定仅适用于命题原子的公式称为否定范式(NNF)。
A formula that is a multiary conjunction of multiary disjunctions of literals is in conjunctive normal form (CNF). 作为文字的多重析取的多重合取的公式是合取范式(CNF)。
A formula that is a multiary disjunction of multiary conjunctions of literals is in disjunctive normal form (DNF). 作为文字的多重连词的多重析取的公式是析取范式(DNF)。
NNF#
A formula is in NNF when it consists only \(\neg,\land,\lor\) connectives and \(\neg\) connective used only on propositions(sometimes called atomic formulas).
For example \(((\neg p\and q)\lor(r\land t))\) formula is in NNF, but \((\neg(p\land q)\lor(r\land t))\) formula is not in NNF. \(\neg\) 只能直接用在命题上,才是 NNF。
A literal is either a propositional atom or its negation. Literal 要么是命题原子,要么是它的否定。只能真或者假,不能亦真亦假。
CNF#
A formula is in CNF when it is in form of \(A_1\land A_2\land A_3\land\dots A_n\) where each Ai is in form \(B_1\lor B_2\lor B_3\lor\dots\lor B_n\) where each Bi is proposition or negation of proposition.
A CNF is a conjunction of clauses: $$ C_1,C_2,C_3,\dots,C_n $$ Each clause C is a disjunction of literals: $$ L_1,L_2,L_3,\dots,L_n $$ Each literal is either a plain variable \(v\) or a negated variable \(\neg v\).
DNF#
A formula is in DNF when it is in form of \(A_1\lor A_2\lor A_3\lor\dots \lor A_n\) where each Ai is in form \(B_1\land B_2\land B_3\land \dots\land B_n\) where each \(B_i\) is literal. If formula is in DNF then it is in the NNF also. The same transformation method work for DNF when we swap ⋁,⋀ connectives.
DNF 和 CNF 相当于把 \(\land,\lor\) 互相对换了。
Example
Formula NF \((a\land\neg b)\land(b\lor(\neg c\land\neg\neg a))\) NNF \((a\lor\neg b)\land(b\lor c)\land(b\lor c\lor d\lor e)\) CNF \((a\lor c\lor\neg d\lor e)\rightarrow(a\land c)\lor(b\lor d)\) not a NF \((a\land c\land e)\lor(a\land c)\lor(b\land d)\) DNF
CNF CONVERSION#
Lecture 17 Hoare Logic#
Outline#
- Introduction
- Programming Rules
- Verifying Loops
- Quantifiers & Arrays
- Rules for Array Assignment
Hoare Logic#
A Hoare Triple is a logical statement of the form: $$ ⦇\phi⦈ S ⦇\psi⦈ $$
- Here, \(S\) is a piece of code, and \(\phi\) and \(\psi\) are logical expressions. \(\phi\) is the precondition and \(\psi\) is the postcondition.
This Hoare triple means:
If the program \(S\) is started in a state satisfying the precondition \(\phi\), then it will terminate in a state satisfying the postcondition \(\psi\).
简单理解就是 \(\phi\) 是输入,\(S\) 是函数代码,\(\psi\) 是输出。
Simple examples
Programming Rules#
Hoare logic has rules for each kind of statement that show how the assertions can be moved around a program. Putting these together allow us to formally prove that a program meets its specification. 霍尔逻辑对每种类型的语句都有规则,这些规则显示了断言如何在程序中移动。 把这些放在一起可以让我们正式证明一个程序符合它的规范。
Rules - Assignment#
意味着我们应该使用谓词𝜓并将所有出现的𝑥替换为𝐸。
Some examples: $$ ⦇y=K⦈ x=y; ⦇x=K⦈\ ⦇true⦈ x=5; ⦇x=5⦈\ ⦇x>0⦈ x++; ⦇x>1⦈\ $$
Reminder: FOL operators#
// TODO FOL operators and Semantics for the connectives, Syntax for quantifiers
Rules - Composition#
简单理解为传递性
Examples: $$ ⦇𝑥 = 𝐾⦈ 𝑥 = 0; 𝑦 = 𝑥; ⦇𝑥 = 0 ∧ 𝑦 = 0⦈\ ⦇𝑥 = 𝐴 ∧ 𝑦 = 𝐵⦈ 𝑡 = 𝑥; 𝑥 = 𝑦; 𝑦 = 𝑡; ⦇𝑥 = 𝐵 ∧ 𝑦 = 𝐴⦈ $$
Rules - Selection#
Lecture 24 Dafny#
Specification of example program: “Given positive integers a and b, the program produces in x the product of a and b”
- requires key word take the precondition: caller needs to ensure this to get a meaningful result
- ensures key word take the postcondition: method guarantees this then precondition is met
Look at the example,
| Text Only | |
|---|---|
The caller should not be able to see w method’s body, only its specification.
创建日期: March 16, 2024