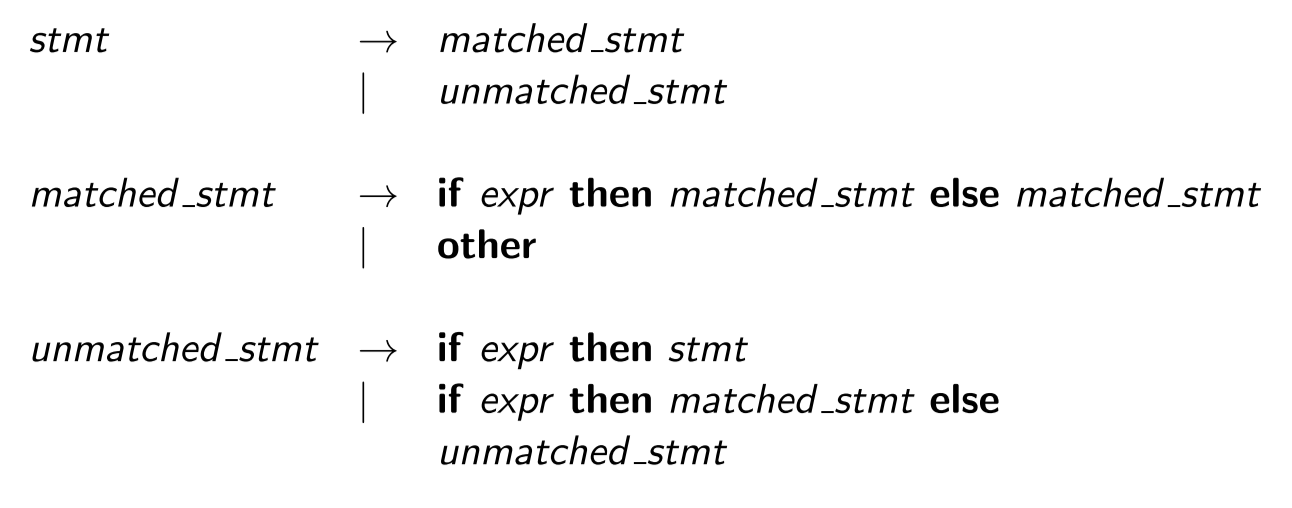Overview#

What is a compiler?#

A compiler is a computer program that translates computer code written in one programming language (the source language) into another language (the target language). -- From Wikipedia

编译器就是将一种编程语言翻译成另一种编程语言的程序。

Goals of this course#

Knowledge:
basic understandings about how a compiler works (theoretically). 关于编译器如何工作的基本理解
understand some of the formal language theories. 了解一些正式的语言理论
be familiar with compiler analysis and optimization techniques 熟悉编译器分析和优化技术
Tools:
know how to use different tools for building compilers. 知道如何使用不同的工具来构建编译器
Extension:
be able to design and write your own programming language. 能够设计和编写自己的编程语言
work on a larger software project (compiler is big)! 处理一个更大的软件项目

Recommended textbook (the dragon book):

[Compilers - principles, techniques and tools ] by Aho, Lam, Sethi, and Ullman.

Chapters:1 - 10 (and not all sections).

Topic Overview#

Lexical analysis 词法分析
Syntactic analysis 句法分析
Semantic analysis 语义分析
Code generation 代码生成
Optimisation 优化

Course Assessment#

Exam: 70-80% We will do e.g., exercises, discussions, etc. CA: 20-30% More about this later

Lecture-1 Intro to Compiler#

What does a compiler do?

It reads in a high level program (close to human language), and transforms it into target code (only machine can understand). The process of transformation is called compilation.

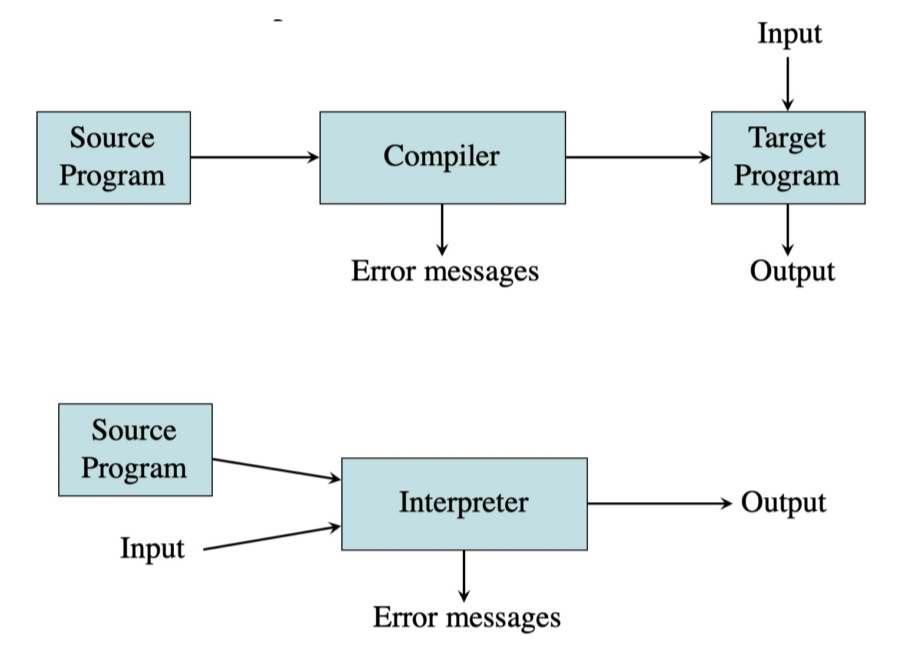
Compiler vs. Interpreter#

The machine-language target program produced by a compiler is usually much faster than an interpreter at mapping inputs to outputs. However, an interpreter can usually give better error diagnostics than a compiler. 在将输入映射到输出时，编译器生成的机器语言目标程序通常比解释器快得多。但是，解释器通常可以提供比编译器更好的错误诊断。

Instead of producing a target program as a translation, an interpreter performs the operations implied by the source program. For an assignment statement, an interpreter might just build a tree and carry out the operations at the nodes as it “walks” the tree. Interpreters are frequently used to execute command languages, since each operator executed in a command language is usually an invocation of a complex routine such as an editor or compiler. For example, JavaScript, python, Matlab, etc. 解释器不是将目标程序生成为翻译，而是执行源程序隐含的操作。对于赋值语句，解释器可能只是构建一棵树并在“遍历”树时在节点处执行操作。解释器经常用于执行命令语言，因为在命令语言中执行的每个运算符通常是对复杂例程（例如编辑器或编译器）的调用。例如，JavaScript、python、Matlab 等。

Analysis and Synthesis#

There are two parts to compilation: analysis and synthesis.

The analysis part (front end) breaks up the source program into pieces and imposes a grammatical structure on them. It uses this structure to create an intermediate representation of the source program. 分析部分(前端)将源程序分解成小块，并对其施加语法结构。它使用这个结构来创建源程序的中间表示。

The synthesis part (back end) constructs the desired target program from the intermediate representation and the information in the symbol table. 合成部分(后端)从中间表示和符号表中的信息构造所需的目标程序。

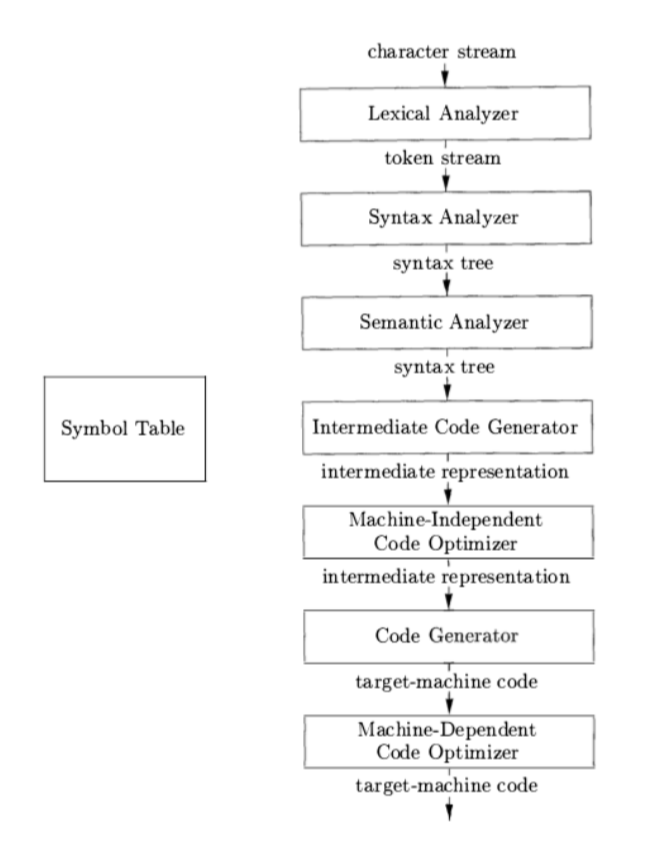
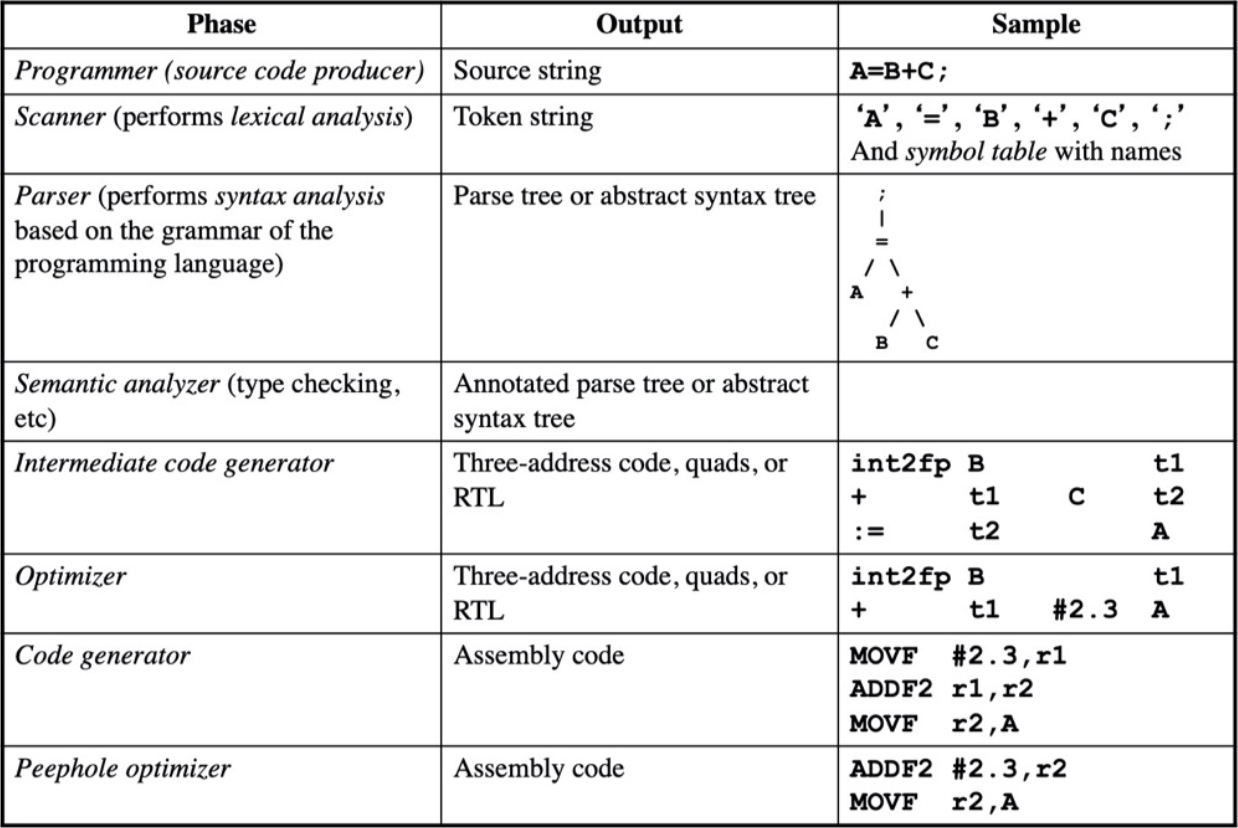
Phases of a Compiler#

character stream -->

Lexical Analyzer 词法分析

--> token stream -->

Syntax Analyzer 语法分析

--> syntax tree -->

Semantic Analyzer 语义分析

--> syntax tree -->

Intermedia Code Generator 中间代码生成器

--> intermediate representation -->

Machine-Independent Code Optimizer 与机器无关的代码优化器

--> intermedia representation -->

Code Generator 代码生成器

--> target-machine code -->

Machine-Dependent Code Optimizer 机器相关代码优化器

--> target-machine code

Tools for manipulating source programs#

Structure editors. A structure editor takes as input a sequence of commands to build a source program. It also analyses the program text. 结构编辑器将一系列命令作为输入来构建源程序。它还分析程序文本。

Pretty printers. A pretty printer analyses a program and prints it in such a way that the structure of the program becomes clearly visible. For example, an amount of indentation proportional to the depth of their nesting structures. 优秀的打印器会分析程序并以程序结构清晰可见的方式打印它。例如，缩进量与其嵌套结构的深度成正比。

Static checkers. A static checker reads a program, analyses it, and attempts to discover potential bugs without running the program. For example, a static checker may detect that parts of the source program can never be executed, or that a certain variable might be used before being defined. 静态检查器读取程序，对其进行分析，并尝试在不运行程序的情况下发现潜在的错误。例如，静态检查器可能会检测到源程序的某些部分永远无法执行，或者某个变量可能在定义之前使用。

Design issues#

Correctness: 正确性
correct output 正确的输出
error report and recovery 错误报告和恢复
Efficiency: 效率
compile time must be reasonable (fast) 编译时间必须合理 (够快)
code generation must be efficient (more efficient code generation might take longer to compile) 代码生成必须高效 (更高效的代码生成可能需要更长的编译时间)
Usability: 可用性
provide a good way of debugging (debugger) 提供一种很好的调试方式

Important Stages#

Front-end:
lexical analysis 词法分析
syntactic analysis 语法分析
semantic analysis 语义分析
Back-end:
optimisation 优化
code generation 代码生成

Each stage has an error report routine. It reports any kind of errors or warnings (according to configuration) during the compilation. 每个阶段都有一个错误报告例程。它在编译期间报告任何类型的错误或警告（根据配置）。

Lecture 7 Grammar#

For Regular Expressions and Context-Free Grammars,

Every construct that can be described by a regular expression can also be described by a grammar. 正则 == DFA == NFA --> CFG == PDA.

For example, the regular expression $(a|b)^*abb$, can be captured by the following grammer: $$ A_0 \rightarrow & aA_0 | bA_0 | aA_1\ A_1 \rightarrow & bA_2\ A_2 \rightarrow & bA_3\ A_3 \rightarrow & \epsilon\ $$

Eliminating Ambiguity#

Sometimes an ambiguous grammar can be rewritten to eliminate the ambiguity. Consider the following grammar (“dangling-else”),

上面的语法是歧义 (ambiguous) 的，因为对于字符串 $if\ E_1\ then\ if\ E_2\ then\ S_1\ else\ S_2$，我们可以有两个解析树 (parse trees)。我们可以重写语法以消除歧义 (eliminate ambiguity)。

Left Recursion#

A grammar is left recursive 左递归 if it has a nonterminal 非终止符 $A$ such that there is a derivation 推导 $A \Rightarrow^{+} A_{\alpha}$ for some string α. Top-down parsing methods cannot handle left-recursive grammars, so a transformation that eliminates left recursion is needed. 自顶向下解析方法无法处理左递归语法，因此需要进行消除左递归的转换。

Productions of the form, $$ A&\rightarrow &A\alpha\ &|&\beta\ &|&\gamma\ $$ are left recursive.

左递归的坏处在于，当语法中的一个产生式是递归的时，预测解析器会在某些输入上永远循环。

Elimination of Left Recursion#

Given a grammar: $A → Aα | β$. We perform the following transformation. $$ A \rightarrow \beta A'\ A' \rightarrow \alpha A'|\epsilon $$ This is the general rule for eliminating left recursion without changing the set of strings derivable from A. This rule by itself suffices in many grammars.

消除左递归有两个情况：

直接左递归

Given a grammar: $A → Aα | β$. We perform the following transformation. $$ A \rightarrow \beta A'\ A' \rightarrow \alpha A'|\epsilon $$ This is the general rule for eliminating left recursion without changing the set of strings derivable from A. This rule by itself suffices in many grammars. 考虑更一般的情况，假定关于非终结符P的规则为

P→Pα1 / Pα2 /…/ Pαn / β1 / β2 /…/βm

其中，αi（I＝1，2，…，n）都不为ε，而每个βj（j＝1，2，…，m）都不以P开头，将上述规则改写为如下形式即可消除P的直接左递归：

P→β1 P’ / β2 P’ /…/βm P’

P’ →α1P’ / α2 P’ /…/ αn P’ /ε

间接左递归

消除间接左递归的方法是，把间接左递归文法改写为直接左递归文法，然后用消除直接左递归的方法改写文法。

General Rules for Eliminating Left Recursion#

No matter how many $A$−productions there are, we can eliminate immediate left recursion from them by the following technique.

First, we group the A−productions as: $$ A\rightarrow A\alpha_1|A\alpha_2|\dots A\alpha_m|\beta_1|\beta_2|\dots|\beta_n $$ where no $β_i$ begins with an $A$.

Syntax Analysis#

LL(1) Grammar#

Definition#

一个文法 G 是 LL(1) 的，当且仅当 G 的任意两个不同的产生式 $A\rightarrow \alpha|\beta$ 满足下面的条件：

不存在终结符号 $\alpha$ 使得 $\alpha$ 和 $\beta$ 都能够推导出以 $\alpha$ 为开头的串。
$\alpha$ 和 $\beta$ 中最多只有一个可以推导出空串。
如果 $\beta\Rightarrow^*\epsilon$，那么 $\alpha$ 不能推导出任何以 $FOLLOW(A)$ 中某个终结符号开头的串。类似地，如果 $\alpha\Rightarrow^*\epsilon$，那么 $\beta$ 不能推到出任何以 $FOLLOW(A)$ 中某个终结符号开头的串。

前两个条件等价于说 $FIRST(\alpha)$ 和 $FIRST(\beta)$ 是不相交的集合。第三个条件等价于说 $\epsilon$ 在 $FIRST(\beta)$ 中，那么 $FIRST(\alpha)$ 和 $FOLLOW(\beta)$ 是不相交的集合，并且当 $\epsilon$ 在 $FIRST(\alpha)$ 时类似的结论成立。

Predictive Parse Table#

之所以能为 LL(1) 文法构造预测分析表器，原因是只需要检查当前输入符号就可以为一个非终结符号选择正确的产生式。这也是 LL(1) 文法这个名字的本意。

预测分析表

构造方法：对于文法 $G$ 的每个产生式 $A\rightarrow \alpha$，进行如下处理：

For each termination $\alpha$, add $A\rightarrow \alpha$ to $M[A,\alpha]$.
If $FIRST(\alpha)$ contains $\varepsilon$, - for each termination $b$, add $A\rightarrow \alpha$ to $M[A,b]$ - if $\$$ in the set $FOLLOW(A)$, add $A\rightarrow \alpha$ in to $M[A,\$]$ also.

Character#

LL(1) 文法已经可以满足描述大部分程序设计语言构造，虽然在为源语言设计适当的文法时需要小心多加小心。例如，左递归的文法和二义性的文法都不可能是 LL(1) 的

-- Dragon Book

Recap#

对于 LL(1) 文法，我们要消除：

左递归 Left recursion
左因式分解 Left factoring
A property regarding First and Follow.

LR(k) Grammar#

在 LR(k) 语法中，$L$ 表示对输入进行从左到右的扫描，$R$ 表示反向构造出一个最右推导序列。

Shift-reduce grammar analyzer 跟 LR 语法的关系是什么？

SLR#

LR 语法分析器是表格驱动的。

直观地讲，只要存在这样一个从左到右的 shift-reduce 语法分析器，它总是能够在某文法的最右句型的句柄出现在栈顶时识别出这个句柄，那么这个文法就是 LR 的。

只要能够写出某个程序设计语言构造的上下文无关文法，就能构建出识别该构造的 LR 语法分析器。
但确实存在非 LR 的上下文无关文法，但是一般可以避免使用这样的文法。

LR 方法可以构建的文法类是可以使用预测方法或 LL 方法进行语法分析的文法类的真超集。

LR 方法的主要缺点是为一个典型的程序设计语言文法手工构造 LR 分析器的工作量非常大。常见的工具例如 Yacc。

一个 LR 语法分析器通过维护一些状态，用这些状态来表明在语法分析过程中所处的位置，从而做出 shift-reduce 决定。这些状态代表了 "项" item 的集合。一个文法 G 的一个 LR(0) 项是 G 的一个产生式再加上一个位于它体中某处的点。例如，产生式 $A\rightarrow XYZ$ 会产生四个项： $$ A\rightarrow \cdot XYZ\ A\rightarrow X\cdot YZ\ A\rightarrow XY\cdot Z\ A\rightarrow XYZ\cdot $$ 对于产生式 $A\rightarrow\epsilon$ 只产生一个项 $A\rightarrow\cdot$.

为了构造一个文法的规范 LR(0) 项集族，我们定义了一个增广文法 augmented grammar 和两个函数 CLOSURE 和 GOTO。

当且仅当语法分析器要使用规则 $S'\rightarrow S$ 进行规约是，输入符号串被接受。

CLOSURE#

If $I$ is one item in grammar $G$, so that $CLOSURE(I)$ is the item set constructed by following two rules:

Primary, Add each item of $I$ into $CLOSURE(I)$.
If $A\rightarrow\alpha\cdot B\beta$ contained in $CLOSURE(I)$, while the $B\rightarrow\gamma$ is a production, and the item $B\rightarrow\cdot\gamma$ not in the $CLOSURE(I)$, Add the item into. Continuously use this rule util no new item can add into.

我们将感兴趣的 items 分为如下两类：

内核项，包括初始项 $S'\rightarrow ·S$ 以及点不在最左端的所有项。
非内核项，除了 $S'\rightarrow ·S$ 以外点在最左端的所有项。

GOTO#

$GOTO(I,X)$，其中 $I$ 是一个项集而 $X$ 是一个文法符号。$GOTO(I,X)$ 被定义为 $I$ 中所有形如 $[A\rightarrow\alpha·X\beta]$ 的项所对应的项 $[A\rightarrow\alpha X·\beta]$ 的集合的闭包。简单来说，GOTO(I,X) 定义了一个 LR(0) 自动机中的转换，状态对应为项集，GOTO(I,X) 方法描述了当输入为 $X$ 时离开状态 $I$ 的转换。

最后更新: March 16, 2024
创建日期: March 16, 2024